- Research Article
- Open access
- Published:
An upper bound for the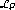 norm of a GCD-related matrix
norm of a GCD-related matrix
Journal of Inequalities and Applications volume 2006, Article number: 25020 (2006)
Abstract
We find an upper bound for the norm of the
norm of the matrix whose
matrix whose entry is
entry is , where
, where and
and are the greatest common divisor and the least common multiple of
are the greatest common divisor and the least common multiple of and
and and where
and where and
and are real numbers. In fact, we show that if
are real numbers. In fact, we show that if and
and , then
, then for all positive integers
for all positive integers , where
, where is the Riemann zeta function.
is the Riemann zeta function.
References
Altinisik E, Tuglu N, Haukkanen P: A note on bounds for norms of the reciprocal LCM matrix. Mathematical Inequalities & Applications 2004,7(4):491–496.
Apostol TM: Introduction to Analytic Number Theory, Undergraduate Texts in Mathematics. Springer, New York; 1976:xii+338.
Bourque K, Ligh S: Matrices associated with classes of arithmetical functions. Journal of Number Theory 1993,45(3):367–376. 10.1006/jnth.1993.1083
Haukkanen P: On thenorm of GCD and related matrices. JIPAM. Journal of Inequalities in Pure and Applied Mathematics 2004,5(3):Article 61, 7 pp..
Haukkanen P, Sillanpää J: Some analogues of Smith's determinant. Linear Multilinear Algebra 1996,41(3):233–244. 10.1080/03081089608818478
Haukkanen P, Wang J, Sillanpää J: On Smith's determinant. Linear Algebra and its Applications 1997, 258: 251–269.
Hong S: GCD-closed sets and determinants of matrices associated with arithmetical functions. Acta Arithmetica 2002,101(4):321–332. 10.4064/aa101-4-2
Korkee I, Haukkanen P: On meet and join matrices associated with incidence functions. Linear Algebra and its Applications 2003, 372: 127–153.
McCarthy PJ: Introduction to Arithmetical Functions, Universitext. Springer, New York; 1986:vii+365.
Sándor J, Crstici B: Handbook of Number Theory, II. Springer, New York; 2004.
Sivaramakrishnan R: Classical Theory of Arithmetic Functions, Monographs and Textbooks in Pure and Applied Mathematics. Volume 126. Marcel Dekker, New York; 1989:xiv+386.
Smith HJS: On the value of a certain arithmetical determinant. Proceedings of the London Mathematical Society 1875/1876, 7: 208–212.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Haukkanen, P. An upper bound for the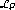 norm of a GCD-related matrix.
J Inequal Appl 2006, 25020 (2006). https://doi.org/10.1155/JIA/2006/25020
norm of a GCD-related matrix.
J Inequal Appl 2006, 25020 (2006). https://doi.org/10.1155/JIA/2006/25020
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/JIA/2006/25020