- Research Article
- Open access
- Published:
Hölder Quasicontinuity in Variable Exponent Sobolev Spaces
Journal of Inequalities and Applications volume 2007, Article number: 032324 (2007)
Abstract
We show that a function in the variable exponent Sobolev spaces coincides with a Hölder continuous Sobolev function outside a small exceptional set. This gives us a method to approximate a Sobolev function with Hölder continuous functions in the Sobolev norm. Our argument is based on a Whitney-type extension and maximal function estimates. The size of the exceptional set is estimated in terms of Lebesgue measure and a capacity. In these estimates, we use the fractional maximal function as a test function for the capacity.
References
Kováčik O, Rákosník J: On spaces
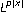 and
and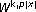 . Czechoslovak Mathematical Journal 1991,41(116)(4):592–618.
. Czechoslovak Mathematical Journal 1991,41(116)(4):592–618.Fan X, Zhao D: On the spaces
 and
and . Journal of Mathematical Analysis and Applications 2001,263(2):424–446. 10.1006/jmaa.2000.7617
. Journal of Mathematical Analysis and Applications 2001,263(2):424–446. 10.1006/jmaa.2000.7617Acerbi E, Mingione G: Regularity results for stationary electro-rheological fluids. Archive for Rational Mechanics and Analysis 2002,164(3):213–259. 10.1007/s00205-002-0208-7
Acerbi E, Mingione G: Regularity results for electrorheological fluids: the stationary case. Comptes Rendus de l'Académie des Sciences - Series I - Mathematics 2002,334(9):817–822.
Diening L, Růžička M: Strong solutions for generalized Newtonian fluids. Journal of Mathematical Fluid Mechanics 2005,7(3):413–450. 10.1007/s00021-004-0124-8
Růžička M: Electrorheological Fluids: Modeling and Mathematical Theory, Lecture Notes in Mathematics. Volume 1748. Springer, Berlin, Germany; 2000:xvi+176.
Růžička M: Modeling, mathematical and numerical analysis of electrorheological fluids. Applications of Mathematics 2004,49(6):565–609. 10.1007/s10492-004-6432-8
Chen Y, Levine S, Rao M: Variable exponent, linear growth functionals in image restoration. SIAM Journal on Applied Mathematics 2006,66(4):1383–1406. 10.1137/050624522
Zhikov VV: On some variational problems. Russian Journal of Mathematical Physics 1997,5(1):105–116.
Bojarski B, Hajłasz P, Strzelecki P: Improved
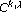 approximation of higher order Sobolev functions in norm and capacity. Indiana University Mathematics Journal 2002,51(3):507–540.
approximation of higher order Sobolev functions in norm and capacity. Indiana University Mathematics Journal 2002,51(3):507–540.Evans LC, Gariepy RF: Measure Theory and Fine Properties of Functions, Studies in Advanced Mathematics. CRC Press, Boca Raton, Fla, USA; 1992:viii+268.
Gutiérrez S: Lusin approximation of Sobolev functions by Hölder continuous functions. Bulletin of the Institute of Mathematics. Academia Sinica 2003,31(2):95–116.
Hajłasz P, Kinnunen J: Hölder quasicontinuity of Sobolev functions on metric spaces. Revista Matemática Iberoamericana 1998,14(3):601–622.
Liu FC: A Luzin type property of Sobolev functions. Indiana University Mathematics Journal 1977,26(4):645–651. 10.1512/iumj.1977.26.26051
Malý J: Hölder type quasicontinuity. Potential Analysis 1993,2(3):249–254. 10.1007/BF01048508
Michael JH, Ziemer WP: A Lusin type approximation of Sobolev functions by smooth functions. In Classical Real Analysis (Madison, Wis., 1982), Contemp. Math.. Volume 42. American Mathematical Society, Providence, RI, USA; 1985:135–167.
Acerbi E, Fusco N: Semicontinuity problems in the calculus of variations. Archive for Rational Mechanics and Analysis 1984,86(2):125–145. 10.1007/BF00275731
Lewis JL: On very weak solutions of certain elliptic systems. Communications in Partial Differential Equations 1993,18(9–10):1515–1537.
Gurka P, Harjulehto P, Nekvinda A: Bessel potential spaces with variable exponent. to appear in Mathematical Inequalities & Applications to appear in Mathematical Inequalities & Applications
Capone C, Cruz-Uribe D, Fiorenza A: The fractional maximal operator on variablespaces. preprint, 2004, http://www.na.iac.cnr.it/
Cruz-Uribe D, Fiorenza A, Neugebauer CJ: The maximal function on variable
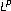 spaces. Annales Academiae Scientiarum Fennicae. Mathematica 2003,28(1):223–238.
spaces. Annales Academiae Scientiarum Fennicae. Mathematica 2003,28(1):223–238.Cruz-Uribe D, Fiorenza A, Neugebauer CJ: Corrections to: "The maximal function on variable
 spaces". Annales Academiae Scientiarum Fennicae. Mathematica 2004,29(1):247–249.
spaces". Annales Academiae Scientiarum Fennicae. Mathematica 2004,29(1):247–249.Diening L: Maximal function on Musielak-Orlicz spaces and generalized Lebesgue spaces. Bulletin des Sciences Mathématiques 2005,129(8):657–700.
Diening L: Maximal function on generalized Lebesgue spaces
 . Mathematical Inequalities & Applications 2004,7(2):245–253.
. Mathematical Inequalities & Applications 2004,7(2):245–253.Kokilashvili V, Samko S: Maximal and fractional operators in weighted
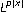 spaces. Revista Matemática Iberoamericana 2004,20(2):493–515.
spaces. Revista Matemática Iberoamericana 2004,20(2):493–515.Lerner AK: Some remarks on the Hardy-Littlewood maximal function on variable
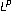 spaces. Mathematische Zeitschrift 2005,251(3):509–521. 10.1007/s00209-005-0818-5
spaces. Mathematische Zeitschrift 2005,251(3):509–521. 10.1007/s00209-005-0818-5Nekvinda A: Hardy-Littlewood maximal operator on
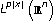 . Mathematical Inequalities & Applications 2004,7(2):255–265.
. Mathematical Inequalities & Applications 2004,7(2):255–265.Musielak J: Orlicz Spaces and Modular Spaces, Lecture Notes in Mathematics. Volume 1034. Springer, Berlin, Germany; 1983:iii+222.
Harjulehto P, Hästö P, Koskenoja M, Varonen S: Sobolev capacity on the space
 . Journal of Function Spaces and Applications 2003,1(1):17–33.
. Journal of Function Spaces and Applications 2003,1(1):17–33.Diening L: Riesz potential and Sobolev embeddings on generalized Lebesgue and Sobolev spaces
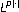 and
and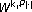 . Mathematische Nachrichten 2004,268(1):31–43. 10.1002/mana.200310157
. Mathematische Nachrichten 2004,268(1):31–43. 10.1002/mana.200310157Harjulehto P, Hästö P: Lebesgue points in variable exponent spaces. Annales Academiae Scientiarum Fennicae. Mathematica 2004,29(2):295–306.
Pick L, Růžička M: An example of a space
 on which the Hardy-Littlewood maximal operator is not bounded. Expositiones Mathematicae 2001,19(4):369–371. 10.1016/S0723-0869(01)80023-2
on which the Hardy-Littlewood maximal operator is not bounded. Expositiones Mathematicae 2001,19(4):369–371. 10.1016/S0723-0869(01)80023-2Kinnunen J, Saksman E: Regularity of the fractional maximal function. The Bulletin of the London Mathematical Society 2003,35(4):529–535. 10.1112/S0024609303002017
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Harjulehto, P., Kinnunen, J. & Tuhkanen, K. Hölder Quasicontinuity in Variable Exponent Sobolev Spaces. J Inequal Appl 2007, 032324 (2007). https://doi.org/10.1155/2007/32324
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/32324
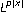 and
and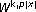 . Czechoslovak Mathematical Journal 1991,41(116)(4):592–618.
. Czechoslovak Mathematical Journal 1991,41(116)(4):592–618. and
and . Journal of Mathematical Analysis and Applications 2001,263(2):424–446. 10.1006/jmaa.2000.7617
. Journal of Mathematical Analysis and Applications 2001,263(2):424–446. 10.1006/jmaa.2000.7617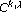 approximation of higher order Sobolev functions in norm and capacity. Indiana University Mathematics Journal 2002,51(3):507–540.
approximation of higher order Sobolev functions in norm and capacity. Indiana University Mathematics Journal 2002,51(3):507–540.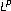 spaces. Annales Academiae Scientiarum Fennicae. Mathematica 2003,28(1):223–238.
spaces. Annales Academiae Scientiarum Fennicae. Mathematica 2003,28(1):223–238. spaces". Annales Academiae Scientiarum Fennicae. Mathematica 2004,29(1):247–249.
spaces". Annales Academiae Scientiarum Fennicae. Mathematica 2004,29(1):247–249. . Mathematical Inequalities & Applications 2004,7(2):245–253.
. Mathematical Inequalities & Applications 2004,7(2):245–253.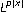 spaces. Revista Matemática Iberoamericana 2004,20(2):493–515.
spaces. Revista Matemática Iberoamericana 2004,20(2):493–515.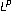 spaces. Mathematische Zeitschrift 2005,251(3):509–521. 10.1007/s00209-005-0818-5
spaces. Mathematische Zeitschrift 2005,251(3):509–521. 10.1007/s00209-005-0818-5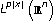 . Mathematical Inequalities & Applications 2004,7(2):255–265.
. Mathematical Inequalities & Applications 2004,7(2):255–265. . Journal of Function Spaces and Applications 2003,1(1):17–33.
. Journal of Function Spaces and Applications 2003,1(1):17–33.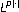 and
and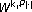 . Mathematische Nachrichten 2004,268(1):31–43. 10.1002/mana.200310157
. Mathematische Nachrichten 2004,268(1):31–43. 10.1002/mana.200310157 on which the Hardy-Littlewood maximal operator is not bounded. Expositiones Mathematicae 2001,19(4):369–371. 10.1016/S0723-0869(01)80023-2
on which the Hardy-Littlewood maximal operator is not bounded. Expositiones Mathematicae 2001,19(4):369–371. 10.1016/S0723-0869(01)80023-2