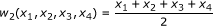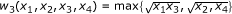- Research
- Open access
- Published:
Gregus type fixed points for a tangential multi-valued mappings satisfying contractive conditions of integral type
Journal of Inequalities and Applications volume 2011, Article number: 3 (2011)
Abstract
In this article, we define a tangential property which can be used not only for single-valued mappings but also for multi-valued mappings, and used it in the prove for the existence of a common fixed point theorems of Gregus type for four mappings satisfying a strict general contractive condition of integral type in metric spaces. Our theorems generalize and unify main results of Pathak and Shahzad (Bull. Belg. Math. Soc. Simon Stevin 16, 277-288, 2009) and several known fixed point results.
Introduction
The Banach Contraction Mapping Principle, appeared in explicit form in Banach's thesis in 1922 [1] (see also [2]) where it was used to establish the existence of a solution for an integral equation. Since then, because of its simplicity and usefulness, it has become a very popular tool in solving existence problems in many branches of mathematical analysis. Banach contraction principle has been extended in many different directions, see [3–5], etc. In 1969, the Banach's Contraction Mapping Principle extended nicely to set-valued or multivalued mappings, a fact first noticed by Nadler [6]. Afterward, the study of fixed points for multi-valued contractions using the Hausdorff metric was initiated by Markin [7]. Later, an interesting and rich fixed point theory for such mappings was developed (see [[8–13]]). The theory of multi-valued mappings has applications in optimization problems, control theory, differential equations, and economics.
In 1982, Sessa [14] introduced the notion of weakly commuting mappings. Jungck [15] defined the notion of compatible mappings to generalize the concept of weak commutativity and showed that weakly commuting mappings are compatible but the converse is not true [15]. In recent years, a number of fixed point theorems have been obtained by various authors utilizing this notion. Jungck further weakens the notion of compatibility by introducing the notion of weak compatibility and in [16] Jungck and Rhoades further extended weak compatibility to the setting of single-valued and multivalued maps. In 2002, Aamri and Moutawakil [17] defined property (E.A). This concept was frequently used to prove existence theorems in common fixed point theory. Three years later, Liu et al.[18] introduced common property (E.A). The class of (E.A) maps contains the class of noncompatible maps. Recently, Pathak and Shahzad [19] introduced the new concept of weak tangent point and tangential property for single-valued mappings and established common fixed point theorems.
The aim of this article is to develop a tangential property, which can be used only single-valued mappings, based on the work of Pathak and Shahzad [19]. We define a tangential property, which can be used for both single-valued mappings and multi-valued mappings, and prove common fixed point theorems of Gregus type for four mappings satisfying a strict general contractive condition of integral type.
Preliminaries
Throughout this study (X, d) denotes a metric space. We denote by CB(X), the class of all nonempty bounded closed subsets of X. The Hausdorff metric induced by d on CB(X) is given by

for every A, B ∈ CB(X), where d(a, B) = d(B, a) = inf{d(a, b): b ∈ B} is the distance from a to B ⊆ X.
Definition 2.1. Let f : X → X and T : X → CB(X).
-
1.
A point x ∈ X is a fixed point of f (respecively T ) iff fx = x (respecively x ∈ Tx).
The set of all fixed points of f (respecively T) is denoted by F (f) (respecively F (T)).
-
2.
A point x ∈ X is a coincidence point of f and T iff fx ∈ Tx.
The set of all coincidence points of f and T is denoted by C(f, T).
-
3.
A point x ∈ X is a common fixed point of f and T iff x = fx ∈ Tx.
The set of all common fixed points of f and T is denoted by F (f, T).
Definition 2.2. Let f : X → X and g : X → X. The pair (f, g) is said to be
-
(i)
commuting if fgx = gfx for all x ∈ X;
-
(ii)
weakly commuting [14] if d(fgx, gfx) ≤ d(fx, gx) for all x ∈ X;
-
(iii)
compatible [15] if limn→∞d(fgx n , gfx n ) = 0 whenever {x n } is a sequence in X such that

for some z ∈ X;
-
(iv)
weakly compatible [20] fgx = gfx for all x ∈ C(f, g).
Definition 2.3. [16] The mappings f : X → X and A : X → CB(X) are said to be weakly compatible fAx = Afx for all x ∈ C(f, A).
Definition 2.4. [17] Let f : X → X and g : X → X. The pair (f, g) satisfies property (E.A) if there exist the sequence {x n } in X such that

See example of property (E.A) in Kamran [21, 22] and Sintunavarat and Kumam [23].
Definition 2.5. [18] Let f, g, A, B : X → X. The pair (f, g) and (A, B) satisfy a common property (E.A) if there exist sequences {x n } and {y n } in X such that

Remark 2.6. If A = f, B = g and {x n } = {y n } in (2), then we get the definition of property (E.A).
Definition 2.7. [19] Let f, g : X → X. A point z ∈ X is said to be a weak tangent point to (f, g) if there exists sequences {x n } and {y n } in X such that

Remark 2.8. If {x n } = {y n } in (3), we get the definition of property (E.A).
Definition 2.9. [19] Let f, g, A, B : X → X. The pair (f, g) is called tangential w.r.t. the pair (A, B) if there exists sequences {x n } and {y n } in X such that

Main results
We first introduce the definition of tangential property for two single-valued and two multi-valued mappings.
Definition 3.1. Let f, g : X → X and A, B : X → CB(X). The pair (f, g) is called tangential w.r.t. the pair (A, B) if there exists two sequences {x n } and {y n } in X such that

for some z ∈ X, then

Throughout this section, ℝ+ denotes the set of nonnegative real numbers.
Example 3.2. Let (ℝ+, d) be a metric space with usual metric d, f, g : ℝ+ → ℝ+ and A, B : ℝ+ → CB(ℝ+) mappings defined by

Since there exists two sequences  and
and  such that
such that

and

Thus the pair (f, g) is tangential w.r.t the pair (A, B).
Definition 3.3. Let f : X → X and A : X → CB(X). The mapping f is called tangential w.r.t. the mapping A if there exist two sequences {x n } and {y n } in X such that

for some z ∈ X, then

Example 3.4. Let (ℝ+, d) be a metric space with usual metric d, f : ℝ+ → ℝ+ and A : ℝ+ → CB(ℝ+) mappings defined by

Since there exists two sequences  and
and  such that
such that

and

Therefore the mapping f is tangential w.r.t the mapping A.
Define Ω = {w : (ℝ+)4 → ℝ+| w is continuous and w(0, x, 0, x) = w(x, 0, x, 0) = x}. There are examples of w ∈ Ω:
-
(1)
w1(x1, x2, x3, x4) = max{x1, x2, x3, x4};
-
(2)
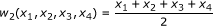
;
-
(3)
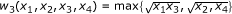
.
Next, we prove our main results.
Theorem 3.5. Let f, g : X → X and A, B : X → CB(X) satisfy

for all x, y ∈ X for which the righthand side of (9) is positive, where 0 < a < 1, α ≥ 0, p ≥ 1, w ∈ Ω and ψ : ℝ+ → ℝ+ is a Lebesgue integrable mapping which is a summable nonnegative and such that

for each ε > 0. If the following conditions (a)-(d) holds:
-
(a)
there exists a point z ∈ f(X) ∩ g(X) which is a weak tangent point to (f, g),
-
(b)
(f, g) is tangential w.r.t (A, B),
-
(c)
ffa = fa, ggb = gb and Afa = Bgb for a ∈ C(f, A) and b ∈ C(g, B),
-
(d)
the pairs (f, A) and (g, B) are weakly compatible.
Then f, g, A, and B have a common fixed point in X.
Proof. It follows from z ∈ f(X) ∩ g(X) that z = fu = gv for some u, v ∈ X. Using that a point z is a weak tangent point to (f, g), there exist two sequences {x n } and {y n } in X such that

Since the pair (f, g) is tangential w.r.t the pair (A, B) and (11), we get

for some D ∈ CB(X). Using the fact z = fu = gv, (11) and (12), we get

We show that z ∈ Bv. If not, then condition (9) implies

Letting n → ∞, we get

Since

which is a contradiction. Therefore z ∈ Bv. Again, we claim that z ∈ Au. If not, then condition (9) implies

Letting n → ∞, we get

Since

which is a contradiction. Thus z ∈ Au.
Now we conclude z = gv ∈ Bv and z = fu ∈ Au. It follows from v ∈ C(g, B), u ∈ C(f, A) that ggv = gv, ffu = fu and Afu = Bgv. Hence gz = z, fz = z and Az = Bz.
Since the pair (g, B) is weakly compatible, gBv = Bgv. Thus gz ∈ gBv = Bgv = Bz. Similarly, we can prove that fz ∈ Az. Consequently, z = fz = gz ∈ Az = Bz. Therefore, the maps f, g, A and B have a common fixed point. □
If we setting w in Theorem 3.5 by  then we get the following corollary:
then we get the following corollary:
Corollary 3.6. Let f, g : X → X and A, B : X → CB(X) satisfy

for all x, y ∈ X for which the righthand side of (20) is positive, where 0 < a < 1, α ≥ 0, p ≥ 1 and ψ : ℝ+ → ℝ+ is a Lebesgue integrable mapping which is a summable nonnegative and such that

for each ε > 0. If the following conditions (a)-(d) holds:
-
(a)
there exists a point z ∈ f(X) ∩ g(X) which is a weak tangent point to (f, g),
-
(b)
(f, g) is tangential w.r.t (A, B),
-
(c)
f fa = fa, ggb = gb and Afa = Bgb for a ∈ C(f, A) and b ∈ C(g, B),
-
(d)
the pairs (f, A) and (g, B) are weakly compatible.
Then f, g, A, and B have a common fixed point in X.
If we setting w in Theorem 3.5 by  and p = 1, then we get the following corollary:
and p = 1, then we get the following corollary:
Corollary 3.7. Let f, g : X → X and A, B : X → CB(X) satisfy

for all x, y ∈ X for which the righthand side of (22) is positive, where 0 < a < 1, α ≥ 0 and ψ : ℝ+ → ℝ+ is a Lebesgue integrable mapping which is a summable nonnegative and such that

for each ε > 0. If the following conditions (a)-(d) holds:
-
(a)
there exists a point z ∈ f(X) ∩ g(X) which is a weak tangent point to (f, g),
-
(b)
(f, g) is tangential w.r.t (A, B),
-
(c)
f fa = fa, ggb = gb and Afa = Bgb for a ∈ C(f, A) and b ∈ C(g, B),
-
(d)
the pairs (f, A) and (g, B) are weakly compatible.
Then f, g, A, and B have a common fixed point in X.
If α = 0 in Corollary 3.7, we get the following corollary:
Corollary 3.8. Let f, g : X → X and A, B : X → CB(X) satisfy

for all x, y ∈ X for which the righthand side of (24) is positive, where 0 < a < 1 and ψ : ℝ+ → ℝ+ is a Lebesgue integrable mapping which is a summable nonnegative and such that

for each ε > 0. If the following conditions (a)-(d) holds:
-
(a)
there exists a point z ∈ f(X) ∩ g(X) which is a weak tangent point to (f, g),
-
(b)
(f, g) is tangential w.r.t (A, B),
-
(c)
f fa = fa, ggb = gb and Afa = Bgb for a ∈ C(f, A) and b ∈ C(g, B),
-
(d)
the pairs (f, A) and (g, B) are weakly compatible.
Then f, g, A, and B have a common fixed point in X.
If α = 0, g = f and B = A in Corollary 3.7, we get the following corollary:
Corollary 3.9. Let f : X → X and A : X → CB(X) satisfy

for all x, y ∈ X for which the righthand side of (26) is positive, where 0 < a < 1 and ψ : ℝ+ → ℝ+ is a Lebesgue integrable mapping which is a summable nonnegative and such that

for each ε > 0. If the following conditions (a)-(d) holds:
-
(a)
there exists a sequence {x n } in X such that limn→∞fx n ∈ X,
-
(b)
f is tangential w.r.t A,
-
(c)
f fa = fa for a ∈ C(f, A),
-
(d)
the pair (f, A) is weakly compatible.
Then f and A have a common fixed point in X.
If ψ (t) = 1 in Corollary 3.7, we get the following corollary:
Corollary 3.10. Let f, g : X → X and A, B : X → CB(X) satisfy

for all x, y ∈ X for which the righthand side of (28) is positive, where 0 < a < 1 and α ≥ 0. If the following conditions (a)-(d) holds:
-
(a)
there exists a point z ∈ f(X) ∩ g(X) which is a weak tangent point to (f, g),
-
(b)
(f, g) is tangential w.r.t (A, B),
-
(c)
f fa = fa, ggb = gb and Afa = Bgb for a ∈ C(f, A) and b ∈ C(g, B),
-
(d)
the pairs (f, A) and (g, B) are weakly compatible.
Then f, g, A, and B have a common fixed point in X.
If ψ(t) = 1 and α = 0 in Corollary 3.7, we get the following corollary:
Corollary 3.11. Let f, g : X → X and A, B : X → CB(X) satisfy

for all x, y ∈ X for which the righthand side of (29) is positive, where 0 < a < 1. If the following conditions (a)-(d) holds:
-
(a)
there exists a point z ∈ f(X) ∩ g(X) which is a weak tangent point to (f, g),
-
(b)
(f, g) is tangential w.r.t (A, B),
-
(c)
f fa = fa, ggb = gb and Afa = Bgb for a ∈ C(f, A) and b ∈ C(g, B),
-
(d)
the pairs (f, A) and (g, B) are weakly compatible.
Then f, g, A, and B have a common fixed point in X.
If ψ(t) = 1, α = 0, g = f, and B = A in Corollary 3.7, we get the following corollary:
Corollary 3.12. Let f : X → X and A : X → CB(X) satisfy

for all x, y ∈ X for which the righthand side of (30) is positive, where 0 < a < 1. If the following conditions (a)-(d) holds:
-
(a)
there exists a sequence {x n } in X such that limn→∞fx n ∈ X,
-
(b)
f is tangential w.r.t A,
-
(c)
f fa = fa for a ∈ C(f, A),
-
(d)
the pair (f, A) is weakly compatible.
Then f and A have a common fixed point in X.
Define Λ = {λ : (ℝ+)5 → ℝ+| λ is continuous and λ(0, x, 0, x, 0) = λ(x, 0, x, 0, 0) = kx where 0 < k < 1}.
Theorem 3.13. Let f, g : X → X and A, B : X → CB(X) satisfy

for all x, y ∈ X for which the righthand side of (31) is positive, where α ≥ 0, p ≥ 1, λ ∈ Λ and ψ : ℝ+ → ℝ+ is a Lebesgue integrable mapping which is a summable nonnegative and such that

for each ε > 0. If the following conditions (a)-(d) holds:
-
(a)
there exists a point z ∈ f(X) ∩ g(X) which is a weak tangent point to (f, g),
-
(b)
(f, g) is tangential w.r.t (A, B),
-
(c)
f fa = fa, ggb = gb and Afa = Bgb for a ∈ C(f, A) and b ∈ C(g, B),
-
(d)
the pairs (f, A) and (g, B) are weakly compatible.
Then f, g, A, and B have a common fixed point in X.
Proof. Since z ∈ f(X) ∩ g(X), z is a weak tangent point to (f, g) and the pair (f, g) is tangential w.r.t the pair (A, B). It follows similarly Theorem 3.5 that there exist sequences {x n } and {y n } in X such that

for some D ∈ CB(X). We claim that z ∈ Bv. If not, then condition (31) implies

Letting n → ∞, we get

Since

which is a contradiction. Therefore z ∈ Bv. Again, we claim that z ∈ Au. If not, then condition (31) implies

Letting n →∞, we get

Since

which is a contradiction. Thus z ∈ Au.
Now we conclude z = gv ∈ Bv and z = fu ∈ Au. It follows from Theorem 3.5 that z = fz = gz ∈ Az = Bz. Therefore the maps f, g, A and B have a common fixed point. □
References
Banach S: Sur les opérations dans les ensembles abstraits et leurs applications aux équations intégrales. Fund Mathb 1922, 3: 133–181.
Caccioppoli R: Un teorema generale sull esistenza di elementi uniti in una trasformazione funzionale. Rend Accad Lincei 1930, 11: 794–799. (Italian)
Branciari A: A fixed point theorem for mappings satisfying a general contractive condition of integral type. Int J Math Math Sci 2002, 29: 531–536. 10.1155/S0161171202007524
Shahzad N: Invariant approximation and R-subweakly commuting maps. J Math Anal Appl 2001, 257: 39–45. 10.1006/jmaa.2000.7274
Vijayaraju P, Rhoades BE, Mohanraj R: A fixed point theorem for a pair of maps satisfying a general contractive condition of integral type. Int J Math Math Sci 2005, 15: 2359–2364.
Nadler SB Jr: Multivalued contraction mappings. Pac J Math 1969, 30: 475–488.
Markin JT: Continuous dependence of fixed point sets. Proc Am Math Soc 1973, 38: 545–547. 10.1090/S0002-9939-1973-0313897-4
Aubin JP, Siegel J: Fixed point and stationary points of dissipative multi-valued maps. Proc Am Math Soc 1980, 78: 391–3980. 10.1090/S0002-9939-1980-0553382-1
Covitz H, Nadler SB Jr: Multi-valued contraction mappings in generalized metric space. Israel J Math 1970, 8: 5–11. 10.1007/BF02771543
Sintunavart W, Kumam P: Weak condition for generalized multi-valued ( f , α , β )-weak contraction mappings. Appl Math Lett 2011, 24: 460–465. 10.1016/j.aml.2010.10.042
Sintunavart W, Kumam P: Coincidence and common fixed points for generalized contraction multi-valued mappings. J Comput Anal Appl 2011,13(2):362–367.
Sintunavarat W, Kumam P, Patthanangkoor P: Common random fixed points for multivalued random operators without S - and T -weakly commuting random operators. Random Oper Stoc Eqs 2009, 17: 381–388. 10.1515/ROSE.2009.022
Wang T: Fixed point theorems and fixed point stability for multivalued mappings on metric spaces. J Nanjing Univ Math Baq 1989, 6: 16–23.
Sessa S: On a weak commutativity condition of mappings in fixed point considerations. Publ Inst Math 1982,32(46):149–153.
Jungck G: Compatible mappings and common fixed points. Int J Math Math Sci 1986, 9: 771–779. 10.1155/S0161171286000935
Jungck G, Rhoades BE: Fixed points for set valued functions without continuity. Indian J Pure Appl Math 1998, 29: 227–238.
Aamri M, ElMoutawakil D: Some new common fixed point theorems under strict contractive conditions. J Math Anal Appl 2002, 270: 181–188. 10.1016/S0022-247X(02)00059-8
Liu Y, Wu J, Li Z: Common fixed points of single-valued and multi-valued maps. Int J Math Math Sci 2005, 19: 3045–3055.
Pathak HK, Shahzad N: Gregus type fixed point results for tangential mappings satisfying contractive conditions of integral type. Bull Belg Math Soc Simon Stevin 2009, 16: 277–288.
Jungck G: Common fixed points for non-continuous non-self mappings on a non-numeric spaces. Far East J Math Sci 1996,4(2):199–212.
Kamran T: Coincidence and fixed points for hybrid strict contractions. J Math Anal Appl 2004, 299: 235–241. 10.1016/j.jmaa.2004.06.047
Kamran T: Multivalued f -weakly Picard mappings. Nonlinear Anal 2007, 67: 2289–2296. 10.1016/j.na.2006.09.010
Sintunavart W, Kumam P: Coincidence and common fixed points for hybrid strict contractions without the weakly commuting condition. Appl Math Lett 2009, 22: 1877–1881. 10.1016/j.aml.2009.07.015
Acknowledgements
The first author would like to thank the Research Professional Development Project Under the Science Achievement Scholarship of Thailand (SAST) and the Faculty of Science, KMUTT for financial support during the preparation of this manuscript for Ph.D. Program at KMUTT. Moreover, we also would like to thank the National Research University Project of Thailand's Office of the Higher Education Commission for financial support (under the CSEC project no.54000267). Finally, the authors would like to thank Professor Alberto Cabada for your help and encouragement. Special thanks are also due to the reviewer, who have made a number of valuable comments and suggestions which have improved the manuscript greatly.
The second author is partially supported by the Commission on Higher Education and the Thailand Research Fund under Grant MRG5380044.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
WS designed and performed all the steps of proof in this research and also wrote the paper. PK participated in the design of the study and suggest many good ideas that made this paper possible and helped to draft the first manuscript. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sintunavarat, W., Kumam, P. Gregus type fixed points for a tangential multi-valued mappings satisfying contractive conditions of integral type. J Inequal Appl 2011, 3 (2011). https://doi.org/10.1186/1029-242X-2011-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2011-3